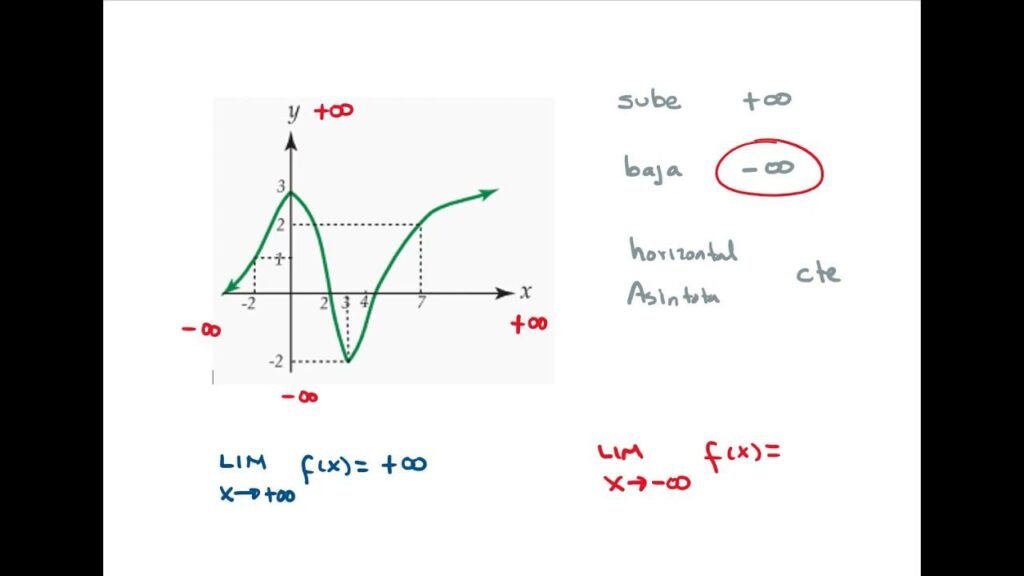
✅ Los límites cuando x tiende a infinito describen el comportamiento de una función f(x) a medida que x crece sin límite, revelando su tendencia o estabilización.
Los límites cuando x tiende a infinito en matemáticas son un concepto fundamental en cálculo que permite analizar el comportamiento de las funciones a medida que su variable independiente se aproxima a valores extremadamente grandes o pequeños. En este contexto, se busca determinar el valor al cual se aproxima la función a medida que la variable x crece sin límites.
Cuando decimos que «x tiende a infinito», estamos haciendo referencia a que x crece sin cesar, ya sea hacia el infinito positivo (+∞) o el infinito negativo (−∞). Esto es crucial en el análisis de funciones racionales, exponenciales y logarítmicas, ya que cada una tiene un comportamiento distinto conforme x se aproxima a infinito. Por ejemplo, para funciones como f(x) = 1/x, el límite es 0 a medida que x tiende a infinito, lo que indica que la función se va acercando a 0.
Ejemplos de límites cuando x tiende a infinito
- Función racional: Para la función f(x) = (2x + 3)/(x + 1), el límite cuando x tiende a infinito es 2. Esto se debe a que los términos de mayor grado dominan el comportamiento de la función.
- Función exponencial: En el caso de f(x) = e^(-x), el límite es 0 cuando x tiende a infinito, ya que la función decae rápidamente.
- Función logarítmica: Para f(x) = log(x), el límite es infinito a medida que x tiende a infinito, lo que indica que la función sigue creciendo, aunque de manera lenta.
Cómo calcular límites al infinito
Para calcular límites cuando x tiende a infinito, se pueden seguir algunos pasos y técnicas:
- Identificar la función y analizar su comportamiento general.
- Si es una función racional, simplificarla dividiendo todos los términos por la mayor potencia de x presente en el denominador.
- Aplicar propiedades de límites, como la regla de L’Hôpital si se presenta una indeterminación.
- Evaluar el resultado final conforme x se aproxima a infinito.
Entender los límites al infinito no solo es clave para el cálculo, sino que también es esencial para el desarrollo de conceptos más complejos en matemáticas avanzadas, como la continuidad, derivadas e integrales. Exploraremos más a fondo estos conceptos y cómo se aplican en diferentes contextos matemáticos.
Aplicaciones y ejemplos prácticos de límites infinitos en la vida real
Los límites infinitos desempeñan un papel crucial no solo en el ámbito académico, sino en diversas áreas de la vida cotidiana y en distintas disciplinas. A continuación, exploraremos algunas aplicaciones y ejemplos prácticos que ilustran la importancia de este concepto matemático.
1. Física: Movimiento y velocidad
En el estudio de la física, los límites infinitos son esenciales para entender el comportamiento de los objetos en movimiento. Por ejemplo, en el cálculo de la velocidad promedio de un objeto que se mueve en línea recta, podemos utilizar el concepto de límite para determinar la velocidad instantánea en un momento específico.
- Si consideramos un objeto que se mueve a una distancia d durante un tiempo t, la velocidad se puede calcular como:
velocidad = d/t. - A medida que t tiende a cero, la velocidad se convierte en la velocidad instantánea.
2. Economía: Modelos de crecimiento exponencial
En economía, los límites se utilizan para analizar el crecimiento de inversiones a largo plazo. Por ejemplo, el interés compuesto se puede expresar matemáticamente como:
- Si A es el monto total, P es el capital inicial, r es la tasa de interés y n es el número de períodos, entonces:
A = P(1 + r/n)^(nt)
A medida que n tiende a infinito, la fórmula se aproxima a:
A = Pe^(rt)
Este concepto permite a los inversores calcular el rendimiento a largo plazo de sus inversiones.
3. Tecnología: Algoritmos y rendimiento
Otro ámbito donde los límites infinitos son relevantes es en el desarrollo de algoritmos en la programación. Los ingenieros de software utilizan límites para evaluar la complejidad computacional de diferentes algoritmos y optimizar su rendimiento. Por ejemplo:
- En el análisis de un algoritmo, podemos observar su tiempo de ejecución cuando el tamaño de entrada n tiende a infinito.
- Esto ayuda a determinar si el algoritmo será eficiente o si necesita mejoras.
4. Biología: Crecimiento poblacional
En el ámbito de la biología, los límites infinitos permiten modelar el crecimiento poblacional de distintas especies. Si consideramos un modelo logístico para el crecimiento poblacional, podemos observar que:
- La población P se describe como:
P(t) = K / (1 + (K – P0) * e^(-rt))
Donde K es la capacidad de carga del ambiente, P0 es la población inicial y r es la tasa de crecimiento. A medida que t tiende a infinito, la población se aproxima a K.
Tabla de comparación de aplicaciones
| Campo | Ejemplo de Aplicación | Importancia |
|---|---|---|
| Física | Velocidad instantánea | Comprender el comportamiento de objetos en movimiento |
| Economía | Interés compuesto | Cálculo de rendimientos a largo plazo |
| Tecnología | Complejidad de algoritmos | Optimizar el rendimiento del software |
| Biología | Crecimiento poblacional | Modelar dinámicas de ecosistemas |
Los límites infinitos ofrecen una visión valiosa en diversas disciplinas, ayudando a formular teorías y modelos que describen con precisión cómo se comportan diferentes sistemas en condiciones extremas. Comprender estos conceptos no solo es fundamental en matemáticas, sino que también es esencial para avanzar en múltiples campos de estudio.
Preguntas frecuentes
¿Qué significa que x tiende a infinito?
Cuando decimos que x tiende a infinito, nos referimos a que x aumenta sin límite, acercándose a valores extremadamente grandes.
¿Cómo se expresa un límite cuando x tiende a infinito?
Se expresa como lim(x→∞) f(x), donde f(x) es la función que se evalúa a medida que x crece indefinidamente.
¿Qué tipos de límites existen?
Existen límites finitos e infinitos. Los límites finitos son aquellos que convergen a un número específico, y los infinitos no tienen un valor definido.
¿Cómo se calcula un límite cuando x tiende a infinito?
Se pueden usar reglas como la regla de L’Hôpital, simplificación de expresiones, o el análisis de términos dominantes.
¿Para qué se utilizan los límites en matemáticas?
Los límites son fundamentales en cálculo, para definir la continuidad, derivadas e integrales, además de ayudar a entender el comportamiento de funciones.
¿Qué pasa si el límite es indeterminado?
Si el límite resulta indeterminado, se pueden aplicar técnicas como factorización o la regla de L’Hôpital para resolverlo.
Puntos clave sobre límites cuando x tiende a infinito:
- Los límites describen el comportamiento de funciones a medida que x se hace muy grande.
- Los límites pueden ser finitos o infinitos.
- Se utilizan en el cálculo de derivadas e integrales.
- La regla de L’Hôpital es útil para resolver límites indeterminados.
- Pueden analizarse los términos dominantes de una función para simplificar el cálculo del límite.
- La comprensión de límites es esencial para el estudio de la continuidad de funciones.
Si te ha quedado alguna duda o quieres compartir tus pensamientos, ¡dejanos tus comentarios! También te invitamos a revisar otros artículos de nuestra web que podrían interesarte.